Toutes les maths en PSI/PSI*
ERRATUM

Un dysfonctionnement indépendant de ma volonté n'a pas permis de rectifier certaines coquilles, pourtant signalées. En implorant votre indulgence, voici un erratum.
page 11, dernière ligne
AU LIEU DE : 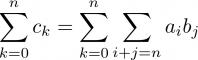
LIRE : 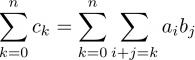
page 54, théorème (propriétés de la distance)
AU LIEU DE LIRE, dans les points 1, 2, 3, ∀x, y ∈ X,
LIRE : ∀x, y ∈ E,
page 59, 2e ligne après la matrice Dx.
AU LIEU DE LIRE : tel que ||P||∞ pour toute P
LIRE : tel que ||P||∞ < M pour toute P
page 72, exercice 3.7
AU LIEU DE LIRE : N1(P) = max1≤k≤n |ak|
LIRE : N1(P) = max0≤k≤n |ak|
page 80, preuve du théorème 1
AU LIEU DE LIRE : Comme de plus u<E> ⊂ F (...), on a u<E> ⊂ F.
LIRE : Comme de plus u<F> ⊂ F (...), on a u<F> = F.
page 81, énoncé du théorème 3, dernière ligne du théorème (signalée par M. El Adnani Mohammed Amine)
AU LIEU DE LIRE : C ∈ ℳn-d, d(K)
LIRE : C ∈ ℳn-d(K)
page 83, preuve du théorème 2, dernière ligne de la page (signalée par M. El Adnani Mohammed Amine)
AU LIEU DE LIRE : φ(x) = 0E + xnφ(d) et ψ(x) = 0E + xnψ(d)
LIRE : φ(x) = 0 + xnφ(d) ψ(x) = 0 + xnψ(d)
page 86, règle de Sarrus (développement d'un déterminant 3x3) (signalée par Julia Welker)
Le premier terme est aei et non aef.
page 132, théorème de la double limite adapté au séries de fonctions, 1er • après "On suppose que" (signalée par M. El Adnani Mohammed Amine)
Il faut enlever "sur tout segment" et lire "la série de fonctions ∑fn converge uniformément sur I".
page 172, exercice 7.11, question 3. (a)
Noter plutôt D la matrice diagonale en question plutôt que Δ (dans le corrigé j'ai laissé D).
page 207, exercice 8.19, question 1
AU LIEU DE LIRE : Montrer que In et Jn sont des intégrales convergentes.
LIRE : Montrer que Jn et Kn sont des intégrales convergentes.
page 246, Méthode 2, dernier paragraphe
AU LIEU DE LIRE : (4) Me2 = e2 + λe3
LIRE : (4) Me2 = e1 + λe2
page 263, 1re ligne (début de la preuve)
AU LIEU DE LIRE : Si r < min(Ra, Rb), alors la série numérique ∑an rn converge absolument (...)
LIRE : Si |z| < min(Ra, Rb), alors la série numérique ∑an zn converge absolument (car |z| < Ra), ainsi que ∑bn zn (car |z| < Rb). On sait alors (cf. chap 1) que leur produit de Cauchy ∑c'n converge absolument, avec c'n = ∑nk=0 ak zk. bn-k zn-k = cn zn et que sa somme vaut (...)
page 271, DSE0 usuels, deux derniers tableaux, 2e ligne,
AU LIEU DE LIRE : 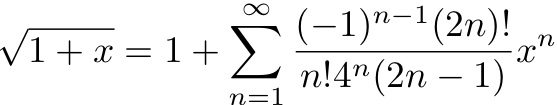
LIRE : 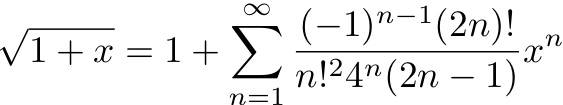
page 271, DSE0 usuels, deux derniers tableaux, avant-dernière ligne,
AU LIEU DE LIRE : 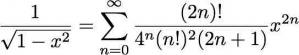
LIRE : 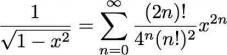
page 292, théorème 2, troisième gros point noir
AU LIEU DE LIRE : [[1, k-1]]
LIRE : [[1, k]]
page 319, théorème 2 (inégalité de Cauchy-Schwarz), dernière ligne
AU LIEU DE LIRE : P(aX + bY = 0) = 1
LIRE : P(aX + bY = c) = 1, avec c un réel.
NB. On dit plutôt que la famille (X,Y) est presque sûrement affinement liée.
page 319, théorème 2 (inégalité de Cauchy-Schwarz), preuve (dernier §)
AU LIEU DE LIRE : Enfin, le cas d'égalité a lieu quand V(X) = 0 (càd quand X = 0 presque sûrement)
LIRE : Enfin, le cas d'égalité a lieu quand V(X) = 0 (càd quand X est constante presque sûrement)
page 332, théorème 2 (loi faible des grands nombres)
Il faut bien sûr rajouter l'hypothèse "X admet une variance finie".
page 351, définiton 1, schéma en fin de page
Erreur de sens de flèche. le bon schéma est :
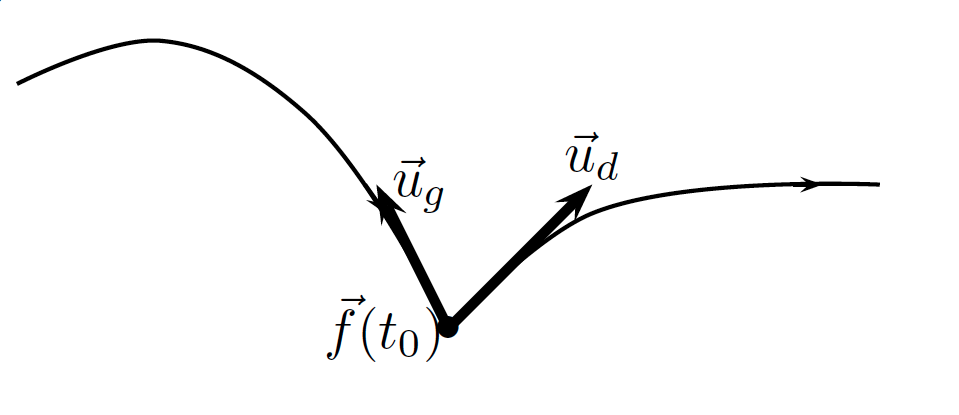
page 352, point 2 de la preuve du théorème, dernière ligne (signalée par M. El Adnani Mohammed Amine)
C'est la limite de [f(t) - f(t0)] / || f(t) - f(t0)|| qu'il faut lire, et non celle de ||f(t) - f(t0)|| / (t - t0)
page 377, fin de la 1re moitié de la page, après "et donc"
AU LIEU DE LIRE :
LIRE :
(idem pour l'égalité finale).
page 379, exemple 2 (signalée par M. El Adnani)
AU LIEU DE LIRE : ∀h ∈ Rⁿ , df(a) = L(h)
LIRE : ∀h ∈ Rⁿ , df(a) • h = L(h)
page 385, preuve du théorème 1 (signalée par M. El Adnani Mohammed Amine)
Il faut lire df(a)•h : j'ai oublié d'écrire ("tel un physicien" dirais-je si j'étais de mauvaise foi) le •h à deux reprises.
page 459, haut de page, fin de la preuve (avant dernière ligne)
AU LIEU DE LIRE : <x|y> = <f(x)|-f(y)> = -<f(x)|f(y)> = <x|y>
LIRE : <x|y> = <f(x)|-f(y)> = -<f(x)|f(y)> = -<x|y>
page 471, corollaire du théoèrme de Cauchy linéaire
AU LIEU DE LIRE : S0 est un sous-espace vectoriel de C1(I, ℳn(K))
LIRE : S0 est un sous-espace vectoriel de C1(I, ℳn,1(K))
page 482, exercice 18.4
Le système à résoudre est
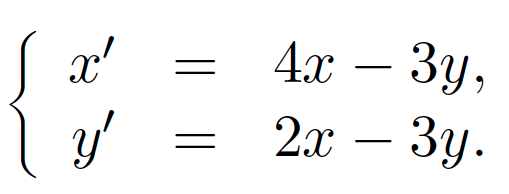
page 506, sous le théorème de Parseval
AU LIEU DE LIRE 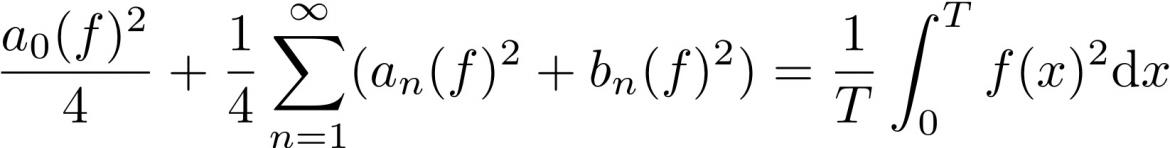
LIRE 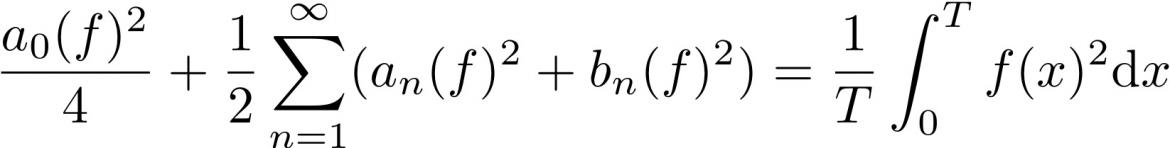
page 506, Exemple d'application
AU LIEU DE LIRE 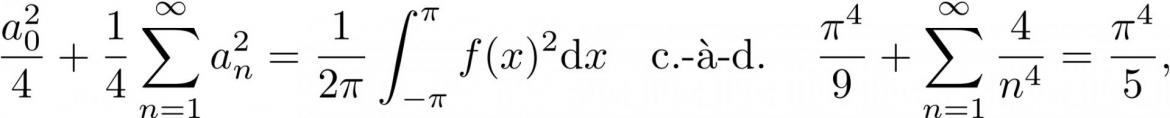
LIRE 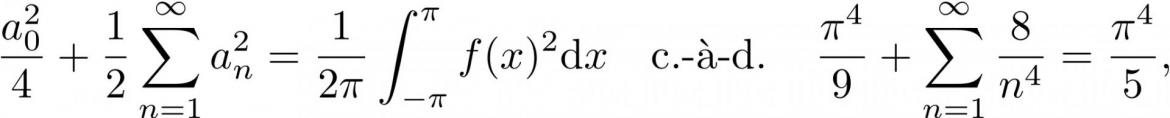
page 543, correction de l'exercice 9, dernière ligne de la page (signalée par Julia Welker)
C'est bien sûr la base (E1,1, E2,1, E1,2, E2,2) qu'il faut considérer.
page 548, correction de l'exercice 2, question 2
AU LIEU DE LIRE : [x-1/4 , x+1/4] est un intervalle de longueur 1/4
LIRE : [x-1/4 , x+1/4] est un intervalle de longueur 1/2
page 551, correction de l'exercice 12, quesiton 3
AU LIEU DE LIRE : Or la fonction X -> AX est continue
LIRE : Or la fonction X -> A-1X est continue
page 552, correction de l'exercice 14, quesiton 2 (avant dernière ligne)
AU LIEU DE LIRE : On aurait une constante k telle que |Pn(0)| ≤ ||Pn||1
LIRE : On aurait une constante k telle que |Pn(0)| ≤ k ||Pn||1
page 563, 3e ligne
AU LIEU DE LIRE : 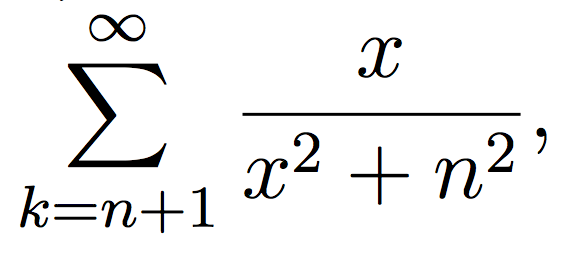
LIRE : 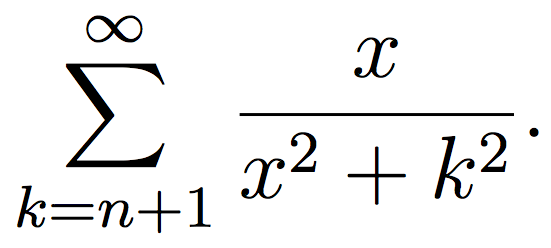
page 569, correction de l'exercice 8,
Puisque E est l'espace des suites convergeant vers 0, λ doit vérifier en plus |λ+1| < 1. Ainsi, le spectre est ]-2,0[ et non R.
page 576, correction de l'exercice 4, question 2 (dernière phrase en dessous du graphique)
AU LIEU DE LIRE : En revanche, elle n'est pas dans ?2 car ∑n2/n2 diverge
LIRE : En revanche, elle n'est pas dans ?2 car ∑n2/n3 diverge.
page 575, correction de l'exercice 3, 2e paragraphe.
L'intégrale est entre 0 et +∞ (et non entre 0 et 1).
page 578, correction de l'exercice 10, question 2
J'ai oublié de reporté de le 2 au dénominateur. Ainsi, la minoration à intégrer est sin2(x)/x ≥ (1 - cos(2x))/(2x) et non sin2(x)/x ≥ (1 - cos(2x))/x
page 609, avant dernière ligne
AU LIEU DE LIRE (1 - 1/(n+1))n -> e
LIRE (1 - 1/(n+1))n -> e-1
page 613, correction de l'exercice 11, quesiton 3
AU LIEU DE LIRE : g(n)(0) = f(n+1)(0)
LIRE : g(n)(0) = f(n+1)(0)/(n+1)
page 635, correction de l'exercice 4 (signalée par M. El Adnani Mohammed Amine)
AU LIEU DE LIRE : | f(x,y) | ≤ x
LIRE : | f(x,y) | ≤ | xy |
page 635, correction de l'exercice 5, question 2 (signalée par M. El Adnani Mohammed Amine)
AU LIEU DE LIRE : Quant aux couples h de la forme (0, y) on a f(th) = 0
LIRE : Quant aux couples h de la forme (0, y) on a f(th) = ty, qui est bien dérivable par rapport à t.
page 654, correction de l'exercice 20, haut de page
LIRE plutôt :

pages 661-662, correction de l'exerice 4


pages 662, correction de l'exerice 9 (dernier § de la question 1, avant dernière ligne).
AU LIEU DE LIRE : limite de y(x) = 0
LIRE : limite de y(x) = +infini.