Conjectures célèbres !
Conjectures célèbres en Mathématiques
Beaucoup pensent que les Mathématiques sont une sorte de matière morte, que l'on enseigne par tradition, et que tout a déjà été trouvé.
Quelle erreur !
Aujourd'hui plus que jamais, la recherche mathématique est très active et très dense. À tel point que deux mathématiciens dans des discplines différentes (Géométrie différentielle et Probabilités par exemple) ont du mal à se comprendre.
Nous présentons ici des conjectures célèbres, c'est-à-dire des résultats que l'on pressent comme étant vrais, mais que l'on n'a pas encore réussi à démontrer. Nous parlerons quand même de deux anciennes conjectures récemment démontrées : leur médiatisation a été spéctaculaire.
Certaines conjectures sont très attendues par la communauté mathématique et des instituts (Clay aux USA) proposent même des primes d'un million de dollars à qui en trouvera la démonstration !
Donc, à vos crayons !
En illustration. Grigori Perelman qui démontra en 2002 la conjecture de Poincaré.
La conjecture de Goldbach
Commençons par quelque chose de simple. Tout du moins dans son énoncé.
Conjecture de Goldbach. Tout entier pair supérieur ou égal à 4 peut s'écrire comme la somme de deux nombres premiers.
Exemple. 16 = 11 + 5 (mais aussi 13 + 3, il n'y a pas unicité).
C'est en 1742 que le mathématicien allemand Christian Goldba
ch (1690-1764) émet cette conjecture. Il écrivit au célèbre L. Euler pour la lui soumettre (en illustration la fameuse lettre).
Aujourd'hui, même avec des ordinateurs puissants, on n'a toujours pas trouvé de contre-exemple.

La conjecture de Syracuse
Continuons sur des mathématiques relativement accessibles techniquement.
Une suite de nombres célèbre est ainsi définie :
- on choisit un entier strcitement positif u0.
- si u0 est pair, on pose u1 = u0/2. Sinon, on pose u1 = 3u0 + 1.
- si u1 est pair, on pose u2 = u1/2. Sinon, on pose u2 = 3u1 + 1.
- on procède de la même façon pour construire un+1 à partir de un.
Exemple. Si on part de u0 = 15, alors u1 = 3×15 + 1 = 46, puis u2 = 46/2 = 23. Le tableau qui suit donne les premiers termes :
| n | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| un | 15 | 46 | 23 | 70 | 35 | 106 | 53 | 160 | 80 | 40 | 20 | 10 | 5 | 16 | 8 | 4 | 2 | 1 | 4 | 2 | ... |
On constate que la suite prend la valeur 1 (pour n = 17). Bien sûr, son comportement est ensuite cyclique : 1 4 2 1 4 2 1 ...
La conjecture de Syracuse consiste à supposer que pour n'importe quelle valeur de u0, la suite correspondante prendra la valeur 1 à un certain moment.
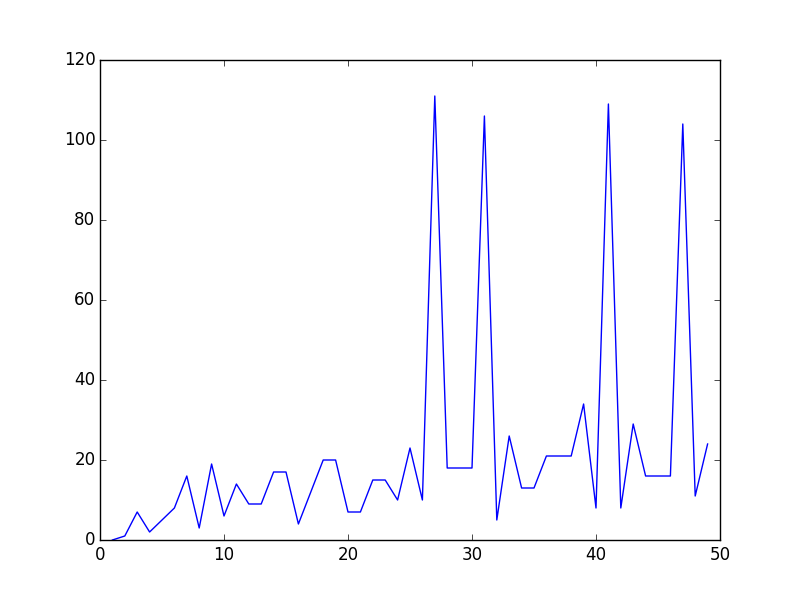
Hauteur de vol. Le plus petit entier n tel que un = 1 s'appelle la hauteur de vol de u0. La hauteur de vol de 15 est donc 17.
On a représenté ci-contre les hauteurs de vol des entiers de 1 à 50.
Cette conjecture a été émise en 1928 par le mathématicien allemand Lothar Collatz (1910-1990). C'est en 1952, après en avoir parlé à l'un de ses collègues, que le problème se diffusa aux USA, dans la ville de Syracuse (Etat de New York, Nord Est de l'Amérique du Nord) : rien à voir avec la Grèce antique donc.
Encore aujourd'hui, on dispose de peu de résultats sur la conjecture de Syracuse. Le célèbre mathématicien hongrois Paul Erdős (prononcer Erdeush) (1913 - 1993) avait dit que les Mathématiques ne sont pas encore prêtes pour de tels problèmes.
 Lothar COLLATZ |
|
La conjecture de Riemann
Voilà une conjecture célèbre qui résiste aux mathématiciens depuis 1859. L'histoire commence par une fonction, notée ζ (zêta), définie par
![]()
expression valable lorsque s est un nombre complexe tel que Re(s) > 1. Par des techniques d'Analyse complexe, on arrive à étendre cette fonction à tous les nombres complexes sauf 1. Bien sûr, l'expression n'est plus celle ci-dessus, mais plus compliquée. C'est cette fonction une fois étendue à C\{1} que l'on appelle la fonction zêta de Riemann.
Fait inattendu : la fonction ζ est très liée aux nombres premiers. En effet, Euler savait déjà, au XVIIIe siècle, que pour tout s > 1,
![]()
où P désigne l'ensemble des nombres premiers.
On peut montrer (relativement facilement) que la fonction ζ : C\{1} ? C s'annule en tous les entiers pairs négatifs : -2, -4, -6, ... Mais il y a d'autres zéros !
La conjecture de Riemann stipule que les zéros de la fonction ζ qui ne sont pas les entiers pairs négatifs (appelés zéros triviaux) ont tous une partie réelle égale à 1/2.
Son lien avec les nombres premiers rend cette conjecture très attrayante : la factorisation en facteurs premiers est en effet le concept de base qui permet de crypter les transactions bancaires et les messages secrets (armée, internet...)
|
Bernhard RIEMANN |

La conjecture de Poincaré (démontrée en 2002)
Une grande partie du travail du mathématicien est de classifier : les nombres, les fonctions, les formes... En Géométrie différentielle, on étudie les courbes (dimension 1), les surfaces (dimension 2), les volumes (dimension 3), et leur généralisation à toute dimension : les variétés.
Parmi les variétés les plus simples figurent les sphères. La sphère de dimension 1 est bien connu : on l'appelle communément un cercle. La sphère de dimension 2 est elle aussi célèbre : c'est la sphère de la Géométrie élémentaire, la surface qui entoure une boule.
La sphère de dimension 2 (de centre 0, de rayon 1), notée S2, peut être décrite comme l'ensemble des points M de l'espace (muni d'un repère orthonormé) dont les coordonnées x, y, z vérifient l'équation x2 + y2 + z2 = 1.
La sphère de dimension 3 (de centre 0, de rayon 1), notée S3, est simplement l'ensemble des points M de l'espace de dimension 4 dont les coordonnées x, y, z, t vérifient l'équation x2 + y2 + z2 + t2 = 1.
Cette sphère S3 est de dimension 3, c'est donc un volume. Mais ce n'est pas la boule contenue dans la sphère S2, de la même façon que la sphère S2 n'est pas le disque contenu dans le cercle S1.
Une représentation (animée pour pallier l'incapacité de notre cerveau à voir la dimension 4) de la sphère S3 est donnée ci-dessous.

Venons-en à la conjecture qu'a émise Henri Poincaré (mathématicien et cousin de Raymond qui fut président de la IIIe République) en 1904.
La sphère S3, comme d'ailleurs toutes les sphères Sn, a des propriétés géométriques naturelles :
- elle est en seul morceau (on dit connexe),
- elle n'a pas de bord (contrairement à la boule dont le bord est la sphère correspondante),
- elle est compacte (fermée et bornée)
- elle est simplement connexe (tout petit cercle tracé sur S3 peut se rétracter continument jusqu'à devenir un point).
La conjecture de Poincaré consiste à affirmer que toute variété connexe, sans bord, compacte et simplement connexe est homéomorphe à la sphère S3.
"Homéomorphe" signifie intuitivement que la variété peut être déformée de façon réversible, sans déchirure, jusqu'à devenir la sphère S3. Pour comprendre cette notion, voici représentées ci-dessous deux variétés homéomorphes : un mug et un tore.

Si V est une variété de dimension n, on peut lui associer une liste de n+1 objets algébriques appelés groupe de (cohomologie de) De Rham de la variété V. La conjecture de Poincaré s'énonce alors en disant que si une variété de dimension 3 a la même liste de groupes de De Rham que S3, alors cette variété est homéomorphe à S3.
Il est étonnant que les mathématiciens aient réussi à démontré ce fait pour toutes les sphères, exceptée S3. Il a fallu attendre 2003 et le mathématicien russe Grigori Perelman pour enfin avoir la caractérisation cohomologique de S3.
Pour l'anecdote, Grigori Perelman a refusé la récompense d'un million de dollars promise par l'institut américain Clay, ainsi que la médaille Fields (équivalent du prix Nobel en Mathématiques).
 |
| Grigori PERELMAN (1966 - ) |

La conjecture de Fermat (démontrée en 1994)
Le lecteur, même collégien, sait qu'il est possible de trouver des entiers a, b, c (non nuls, sinon c'est vraiment trop facile) vérifiant la célèbre relation
a2 + b2 = c2
Pourquoi célèbre ? Parce que cela provient du théorème de Pythagore ! Dans tous les manuels de Mathématiques, on trouve l'exemple du triangle rectangle suivant
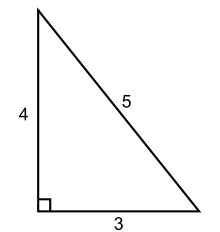
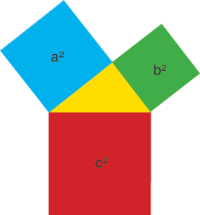
où la relation 32 + 42 = 52 s'interprète en terme de remplissage d'aire : si l'on remplit le carré rouge d'eau, et si l'on retourne la figure, alors l'eau se répartit exactement dans les carrés vert et bleu.
On démontre que le triplet (3,4,5) est très loin d'être la seule solution entière de l'équation a2 + b2 = c2. Bien sûr, tout triplet de la forme (3k, 4k, 5k) avec k un entier non nul quelconque convient aussi, mais c'est un peu facile. Par exemple (5,12,13) est une solution plus pertinente : elle n'est pas proportionnelle à (3,4,5). En fait, il y a même une infinité de solutions non proportionnelles entre elles, mais c'est un autre débat.
On souhaite généraliser ce problème à la dimension 3 : peut-on trouver des entiers non nuls a, b, c tels que a3 + b3 = c3 ? Géométriquement, cela reviendrait à chercher un cube d'arête c pouvant se décomposer en deux petits cubes d'arêtes respectives a et b.
La réponse à ce problème est négative : Euler en a donné la preuve au XVIIIe siècle.
La conjecture de Fermat, consistait à dire que quel que soit l'exposant entier n > 2, il est impossible de trouver des entiers non nuls a, b, c tels que an + bn = cn.
Pierre de Fermat (1601-1665), juriste toulousain et mathématicien amateur de haut niveau, aurait remarqué ce fait, et écrit négligemment dans la marge d'un carnet : « Au contraire, il est impossible de partager soit un cube en deux cubes, soit un bicarré en deux bicarrés, soit en général une puissance quelconque supérieure au carré en deux puissances de même degré : j'en ai découvert une démonstration véritablement merveilleuse que cette marge est trop étroite pour contenir »
Aujourd'hui, on sait que Fermat n'a pu trouver une preuve de ce fait. Sans doute avait-il commis une erreur, commune à l'époque, concernant ce qu'on nomme aujourd'hui les extensions cyclotomiques, mais expliquer cela est hors de propos ici.
Des générations de mathématiciens ont dû attendre 1994 avant que le mathématicien britannique Adrew WILES (1953- ) démontre, de façon spectaculaire et inattendue, cette célèbre conjecture.
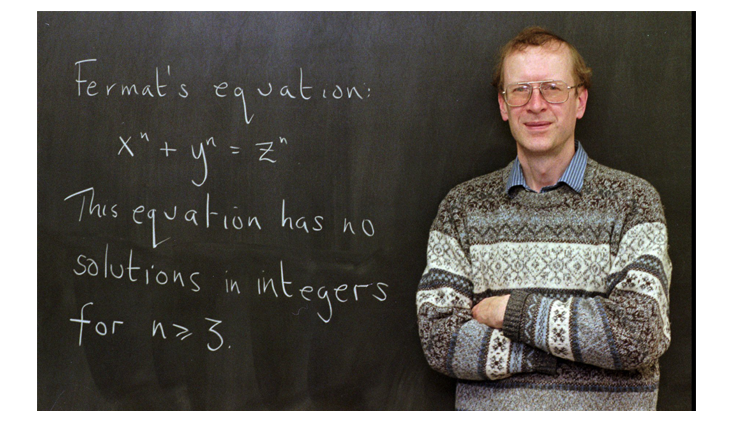
La preuve de Wiles est longue, technique, compliquée, de très haut niveau. Pour la résumer, nous dirions :
- qu'on se ramène au cas où l'exposant n est un nombre premier.
- qu'à toute solution (a, b, c) de l'équation on associe une courbe abstraite très spéciale, appelée courbe elliptique (qui n'a presque aucun rapport avec une ellipse).
- on démontre que ces courbes elliptiques associées à une solution ne peuvent se paramétrer avec des fonctions complexes qualifiées de modulaires.
- mais en fait on démontre que toutes les courbes elliptiques (ou en tout cas celles qui nous intéressent) peuvent se paramétrer avec des fonctions modulaires.
On conclut grâce à un raisonnement par l'absurde : s'il existait une solution, on obtiendrait une courbe elliptique qui est paramétrée par une fonction modulaire alors qu'elle n'est pas censée l'être !
Depuis, la conjecture de Fermat a été rebaptisée théorème de Fermat-Wiles. (Fermat-Wiles Last Theorem en anglais). Bien sûr Andrew WILES a été récompensé par la communauté mathématique (il a obtenu le prix Abel), et son nom a été gravé pour toujours dans l'histoire des Mathématiques.

La quadrature du cercle (démontrée en 1882)
Le problème de la quadrature du cercle est un très vieux défi géométrique : il consiste, étant donné un disque, de construire, à l'aide d'un compas et d'une règle (non graduée) seulement, un carré dont l'aire est égale à celle du disque donné.
Pourquoi cette restriction ? Parce que les Grecs de l'Antiquité considéraient ces deux seuls outils comme "purs", permettant de représenter les deux figures emblématiques de la Géométrie de l'époque : la droite et le cercle.
Les mathématiciens se sont acharnés sur ce problème pendant des siècles, quasiment sans discontinuer. Il faut attendre un outil algébrique moderne pour trancher la question : la notion de groupe. Nous n'expliquerons pas ici ce qu'est un groupe, mais nous disons seulement que ce concept a permis de faire des bons fulgurants en Algèbre.
Voilà comment la quadrature du cercle prit fin :
- On définit la notion de point constructible du plan. C'est un point du plan pouvant être obtenu après un nombre fini d'intersections de droites ou de cercles, à partir du point O(0,0) et I(1,0).
- Un nombre constructible est alors un nombre réel valant l'abscisse d'un point constructible. On peut facilement montrer que la somme et le produit de deux nombres constructibles est un nombre constructible. On peut aussi montrer que si x est un nombre positif constructible, alors sa racine carrée √x l'est aussi (conséquence du théorème de Pythagore). Enfin, si x est un constructible non nul, son inverse 1/x est encore constructible (conséquence du théorème de Thalès).
- Un théorème dû au mathématicien français Pierre-Laurent Wantzel en 1837 énonce que si x est un nombre constructible, alors le plus petit polynôme non nul à coefficients entiers dont x est racine a pour degré une puissance de 2. C'est ici que la théorie des groupes intervient.
- Un résultat totalement indépendant de celui de Wantzel, qui n'a rien à voir avec les groupes, affirme quant à lui que le nombre π n'est racine d'AUCUN polynôme non nul à coefficients entiers. On dit alors que π est un nombre transcendant. C'est un résultat très technique d'Analyse, qui a été montré par le mathématicien allemand Karl Lindemann en 1882.
- On assemble ces deux résultats : l'aire d'un disque de rayon 1 étant de π, s'il était possible de construire un carré d'aire π, le nombre √π qui mesure l'un de ses côtés serait alors constructible, et par suite, π aussi : il serait donc racine d'un certain polynôme non nul (de degré une puissance de 2, mais on s'en fiche ici), ce qui est impossible d'après le théorème de Lindemann.
En conclusion, ce sont les résultats conjoints de Wantzel et de Lindemann qui ont permis de montrer, en 1882, que la quadrature du cercle était impossible.
Bien sûr, si l'on s'autorise d'autres outils que la règle et le compas, on peut arriver à la quadrature du cercle, mais ce n'est plus le problème d'origine. En ajoutant aux cercles et aux droites une courbe inventée par Dinostrate (-300 av JC) on arrive à cette prouesse ! Hélas, si la courbe de Dinostrate se construit point par point grâce à une règle et un compas, cette courbe ne peut être obtenue dans sa totalité en un nombre fini d'étape (il y a une infinité de points sur une courbe !)
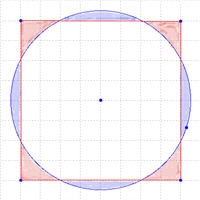
Les 23 problèmes de Hilbert
David HILBERT (1862-1943) est un mathématicien très influent de son époque. Il n'est pas question ici de résumer son œuvre en quelques lignes, mais en 1900, il proposa une liste de 23 grands problèmes mathématiques. Il déclara que la recherche des ses grandes énigmes contribuera à faire de grands progrès en Mathématiques.
Les énoncés de ces 23 problèmes sont souvent techniques et difficiles : ils s'adressent à un public averti. Notons toutefois que la conjecture de Poincaré, la conjecture de Goldbach, l'hypothèse de Riemann (cf. plus haut) font partie de la liste !
le 6e problème se propose d'axiomatiser la Physique, comme on l'a fait pour les Mathématiques. À ce jour, ce problème n'est pas résolu.




