Les surfaces minimales
En Géométrie différentielle, une surface est dite minimale quand elle minimise son aire tout en respectant certaines conditions à son bord. L'exemple le plus parlant est celui des “bulles” de savon que l'on obtient en plongeant un fil métallique dans de l'eau savonneuse.
Des vidéos expliquées faites au Palais de la Découverte : http://www.palais-decouverte.fr/index.php?id=1887
Problème de Plateau : étant donné un bord, existe-t-il une surface minimale s'y appuyant ? y en a-t-il qu'une ?
Bien sûr il faut définir les termes : “bord”, “s'appuyer” et mettre en équation la notion de minimalité d'une aire. Le problème a été étudié par Joseph Plateau (1801-1883), belge.
La courbure moyenne. Sur une surface donnée, on peut tracer des courbes, comme on l'a fait ci-dessous sur un ellipsoïde.
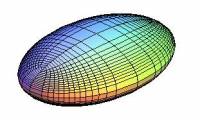
On démontre qu'en chaque point de la surface, il existe deux courbes orthogonales en ce point, dont la courbure est respectivement minimale et maximale. On note κ1 et κ2 ces deux courbures appelées courbure principales au point considéré.
Pour ceux qui connaissent un peu d'Algèbre (niveau Spé), on démontre que ces deux nombres sont les valeurs propres d'un endomorphisme autoadjoint très important associé à la surface : l'endomorphisme de Weingarten.
La courbure de Gauss est 
: c'est le déterminant de l'endomorphisme de Weingarten.
La courbure moyenne est 
: c'est la demi trace de l'endomorphisme de Weingarten.
La courbure moyenne sert à déceler les surfaces minimales : si une surface est minimale alors sa courbure moyenne H est nulle.
Cas des surfaces d'équation cartésienne z = f(x,y) En calculant la courbure moyenne, on trouve que si une telle surface est minimale alors
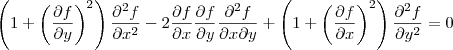
Référence. Elementary Differential Geometry - Andrew Presley - (Ed. Springer)