Défis !

Défi n°1. Démontrer que les suites u(n) = cos(n) et v(n) = sin(n) n'ont pas de limite.
Indication : raisonner par l'absurde et utiliser des formules de trigonométrie.

Défi n°2. Trouver l'expression f(x) d'une fonction définie sur R admettant les droites D : y = -x+3 et D' : y = 2x+1 comme asymptotes obliques respectivement en + et - l'infini. On veut une vraie “formule” et on souhaite que f ne coïncide pas avec ses asymptotes.

Défi n°3. En utilisant exactement quatre chiffres “3” et les opérations connues (+, -, x, /, racines, parenthèses…) écrire le plus possibles de nombres entiers. Exemple : 0 = (3-3) + (3-3).

Défi n°4. Si f est paire et dérivable en 0, montrer que la courbe de f admet une tangente horizontale en 0.

Défi n°5. Dériver 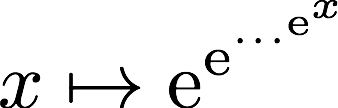 (avec n exponentielles imbriquées).

Défi n°6. Démontrer de trois façons différentes que 0,9999…. = 1.

Défi n°7. Détailler les éléments de l'ensemble ℘(℘({a,b})).

Défi n°8. Démontrer que si 0 = 1 alors Rohart (qui ne sait pas jouer au Tennis) bat Nadal 3 sets à 0.

Défi n°9. Retrouver sans récurrence (ce qui supposerait de connaître le résultat), les expressions donnant 1+2+…+n et 1+q+q²+…+qⁿ.

Défi n°10. Trouver deux fonctions non nulles dont le produit est la fonction nulle. Montrer que ce phénomène n'est pas possible pour les fonctions polynômes.

Défi n°11. On constate que Arctan et th se ressemblent beaucoup. Trouver une transformation simple sur th pour faire coïncider, valeur en 0, asymptotes et tangente en 0. La fonction obtenue est-elle Arctan ?

Défi n°12. Trouver une écriture fractionnaire du réel 25,10181118111811… (Evariste Galois est né le 25/10/1811).

Défi n°13. Trouver une expression (unique, pas "par cas") du terme d'indice n de  la suite 1,1,0,1,1,0,1,1,0,1,1….

Défi n°14. Calculer le volume de la boule de dimension 4, et plus généralement exprimer le volume de la boule de dimension n en fonction des intégrales de Wallis.

Défi n°15. Trouver une application “naturelle” qui va d'un K-espace vectoriel E dans (E*)* (bidual de E, c'est le dual du dual de E). Montrer que c'est un isomorphisme si E est de dimension finie.

Défi n°16. Quand on “superpose” tous les polygones réguliers à n côtés, quand n décrit N*, obtient-on tout le cercle dans lequel ils sont inscrits ? On pourra utiliser les groupes U_n des racines n-ièmes de 1.

Défi n°17. Montrer que la fonction cosinus n'est, sur aucun intervalle aussi petit soit-il, la restriction d'une fonction rationnelle.

Défi n°18. Trouver une fonction qui n'est pas strictement monotone mais qui est une bijection de R dans R.

Défi n°19. Montrer que, quel que soit n, la famille (1, √2, √3, √5, √7, √11, …, √p(n)) où p(n) est le n-ième nombre premier, est une famille libre dans R vu comme Q-espace vectoriel.

Défi n°20. Soit f une fonction de R dans R tel que |f| < 1 et vérifiant f(x+5/6) + f(x) = f(x+1/2) + f(x+1/3) pour tout x. Montrer que f est périodique.

Défi n°21. Trouver deux fonctions périodiques dont la somme n'est pas périodique.

 

PROJECT EULER (en anglais).

De très nombreux problèmes ludiques et motivant.

https://projecteuler.net/about

 

Traduction en français des problèmes 1 à 50 du Project Euler.

http://blog.lucaswillems.com/532/traduction-problemes-1-50-project-euler