La dimension 4

On entend souvent parler de la “4e dimension”, ou “d'espace à 4 dimensions”, sans vraiment savoir ce qu'on entend par “espace” et encore moins par “dimension”. Pour faire simple, la dimension d'un espace est le nombre exact de données chiffrées nécessaires pour décrire parfaitement un objet de cet espace.
Exemple volontairement naïf. Pour écrire une lettre à quelqu'un on doit avoir : 1) son prénom, 2) son nom, 3) son numéro de rue, 4) sa rue, 5) son code postal/ville. L'“espace” des personnes ayant une adresse postale est donc de dimension 5.
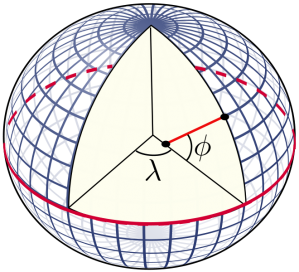
Exemple plus mathématique. Pour décrire un objet sur une sphère, il faut et il suffit de se donner une longitude et une latitude. La sphère est donc un objet de dimension 2.
En revanche, pour décrire un point dans une boule, il faut en plus la distance qui le sépare au centre : la boule est un objet de dimension 3.
Abus de langage fréquent. On dit souvent “espace à 4 dimensions” et c'est une erreur. On doit dire “espace de dimension 4”. On dit de quelqu'un qui pèse 70 kg qu'il est de masse 70 kg, on ne dit pas qu'il a 70 masses !
Qu'est-ce qu'on appelle un "espace" ?
On procède de la façon suivante :
-
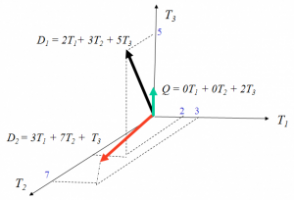
On définit les espaces vectoriels, ce sont des ensembles où l'on peut additionner ses éléments, et les multiplier par des nombres (réels ou complexes). L'adjectif “vectoriel” est là pour rappeler l'analogie avec les vecteurs de la Géométrie du pan ou de l'espace, mais en fait un espace vectoriel peut tout à fait être un ensemble de fonctions (on peut additionner deux fonctions et multiplier une fonction par un nombre). Un espace vectoriel possède un élément très particulier : le vecteur nul.
-
On définit les espaces affines, ce sont intuitivement des espaces vectoriels translatés : dans un espace affine, il n'y a plus d'élément particulier comme le vecteur nul, tous les éléments ont le même rôle. Les éléments d'un espace affine sont appelés des points, par opposition aux éléments d'un espace vectoriel qui sont appelés vecteurs.

-
On définit les variétés, ce sont intuitivement des “espaces courbes”, un peu comme si on tordait un espace affine. Les courbes, les surfaces (sous réserve de régularité) sont des variétés. Tout comme la Terre peut paraître plate quand on la regarde de près, une variété ressemble localement à un espace affine. Bien sûr il faut définir ce qu'on entend par “ressembler”, mais ceci est un cours de Géométrie différentielle de L3/M1.
Qu'est-ce qu'on appelle la "dimension" ?
On définit la dimension d'un espace vectoriel, d'un espace affine, puis d'une variété.
-
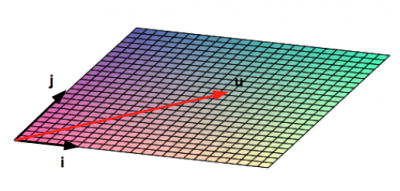
Dans le plan, tout vecteur u peut-être écrit u = a.i + b.j avec i,j deux vecteurs non colinéaires (souvent i est représenté horizontalement, j verticalement, et orthogonaux). On dit alors que la famille (i,j) est une base. Puisqu'il en faut DEUX, on dira que l'ensemble des vecteurs du plan est un espace (vectoriel) de dimension DEUX. Plus généralement on montre que dans un espace vectoriel engendré par un nombre fini de vecteurs, toute base possède le même nombre de vecteurs : cet entier s'appelle la dimension de l'espace vectoriel.
-
Un espace affine est en quelque sorte un espace vectoriel translaté. La dimension de l'espace affine est celle de cet espace vectoriel.
-
Une variété “ressemble” localement à un espace affine. On montre (et c'est assez difficile) que si deux variétés se “ressemblent” alors elles ont même dimension (au moins localement). Cette dimension sera par définition la dimension de la variété.
NB. Pour le lecteur avancé, deux objets “se ressemblent” signifie exactement qu'ils sont “homéomorphes” c.-à-d. qu'il existe une bijection continue de l'un sur l'autre, dont la réciproque est elle aussi continue. Cf. homéomorphisme.
Qu'est-ce que la Relativité générale ?
Au début du XXe siècle Albert Einstein a émis l'hypothèse que l'univers serait une variété de dimension 4 (car un objet est décrit par 3 coordonnées d'espace et une de temps) et que la masse (par exemple celle d'une étoile comme le Soleil) incurvait l'univers, comme une feuille de caoutchouc sur laquelle on poserait une bille d'acier.

En 1915 les physiciens ont effectivement mesuré la déviation des rayons lumineux lors du passage de Mercure entre le Soleil et la Terre. Au lieu d'aller “tout droit” ces rayons ont été déviés par la courbure. L'objet mathématique qui mesure ce phénomène s'appelle le tenseur de courbure de Ricci. On le note Ri,k
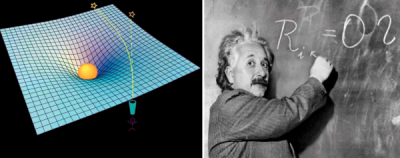
Aujourd'hui on se sert de la Relativité générale dans les GPS pour nous permettre de nous localiser très précisément. Lire par exemple cet article.
Qu'est-ce que la Relativité restreinte ?
Une courbe possède des droites tangentes en chacun de ses points. Une surface possède des plans tangents en chacun de ses points. Une variété, de façon générale, possède en chacun de ses point un espace affine tangent. Celui-ci a la même dimension que la variété. Les phénomènes qui se passent dans l'univers, variété de dimension 4, sont étudiés par la Relativité générale. Ceux qui se répercutent sur l'espace tangent (appelé espace de Minkowski) sont du ressort de la Relativité restreinte.
Cet espace qui n'est autre que R⁴ d'un point de vue algébrique, n'est pas l'espace euclidien habituel : le “produit scalaire” n'est pas défini par la célèbre formule
![]()
mais par :
![]()
où c est la vitesse de la lumière. Ainsi dans cet espace (qualifié de pseudo-euclidien), il existe des vecteurs non nuls, ayant une “norme” nulle. Leur ensemble forme ce qu'on appelle le cône de lumière.
Lire par exemple :
Peut-on voir des objets "à 4 dimensions" ?
Soyons francs et répondons tout de suite : NON. Notre cerveau n'en est pas capable. Ou alors éventuellement en faisant se mouvoir un objet “à 3 dimensions”, le déplacement temporel représentant en quelque sorte “la 4ème dimension”, mais c'est tout aussi frustrant que de représenter un cube en dessinant un carré qui s'élèverait de la face du fond jusqu'à la face du dessus…
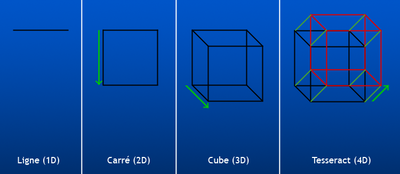
Pour le tesseract (cube de dimension 4), qui par définition est l'ensemble des quadruplets de réels (x,y,z,t) avec x,y,z,t compris entre 0 et 1, on a trouvé différentes astuces pour se l'imaginer :
-
par un “patron”, comme on le ferait pour un cube. Evidemment ce patron est en dimension 3 (tout comme la patron d'un cube est en dimension 2),
-
par un graphe (sommets reliés entre eux par des arêtes).
 |
 |
 |
Seules les dimensions supérieures à 4 nous sont inaccessibles ?
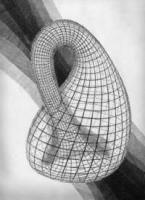
On croit souvent que notre cerveau peut concevoir les dimensions 0 (points), 1 (courbes), 2 (surfaces), et 3 (volumes) et que la limite est la dimension 4. Ceci est FAUX. Notre cerveau ne peut pas concevoir tous les objets de dimension…2 ! L'exemple le plus connu est celui de la bouteille de Klein : on ne peut représenter (en dessin, en verre) cette surface qu'en “trichant”. En réalité (ceci se démontre) le goulot de la bouteille rejoint le fond sans rentrer dans son corps, c.-à-d. sans créer de singularité.
 |
 |
 |
On peut expliquer cela en descendant d'une dimension et en imaginant des petits bonshommes tout plats vivant dans une feuille de papier : ceux-ci ne pourraient concevoir une courbe telle que celle dessinée ci-dessus : ils diraient “mais voyons, c'est impossible, la courbe ne peut pas passer au-dessus d'elle-même sans se recouper !”. Evidemment, puisqu'ils ne conçoivent la dimension 3 ! Eh bien nous, nous sommes des êtres tout plats vivant dans une feuille de dimension 3, et les bouteilles de Klein que l'on dessine ne sont que des ombres de la vraie surface. La bouteille de Klein est une surface (objet de dimension 2) que l'on ne peut pas voir car naturellement plongée dans un espace de dimension 4.
Un théorème dû au mathématicien H. Whitney (en 1936) assure que toute surface peut se plonger dans l'espace R⁴ (espace numérique “plat” de dimension 4). On peut même montrer que toute surface compacte et orientable peut se voir dans R³. La bouteille de Klein étant compacte mais pas orientable (elle ne définit ni intérieur, ni extérieur), il est vain d'essayer de la voir réellement : elle nous est inaccessible.
Des objets célèbres de dimensions diverses
-
Le ruban de Möbius : premier exemple (1858) de surface non orientable : elle n'a qu'un seul bord.
-
La bouteille de Klein : célèbre surface compacte non orientable ne définissant ni intérieur, in extérieur. Décrite par F. Klein en 1882.
-
La sphère S³, qui est l'ensemble des quadruplets (x,y,z,t) de réels vérifiant x²+y²+z²+t²=1. C'est un “volume” (objet de dimension 3) qui est le bord de la boule de dimension 4, on ne peut donc pas la voir ! Elle est célèbre pour avoir fait l'objet de longues recherches concernant la conjecture de Poincaré (démontrée en 2003). Une représentation de cette fameuse sphère est la fibration de Hopf.
-
Le plan projectif : c'est l'ensemble de toutes les droites de l'espace R³ passant par l'origine. Tout comme la bouteille de Klein, c'est une surface (d'où le nom de “plan”) qui est compacte et non orientable. On ne peut donc pas le voir dans R³. Une de ses immersions possibles est la surface de Boy.
 |
 |
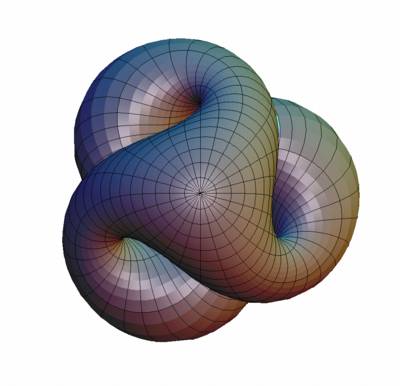 |
| Le ruban de Möbius | La fibration de Hopf | La surface de Boy |
Le mystère de la dimension 4
D'un point du vue algébrique, l'espace numérique R⁴ n'est pas plus compliqué que les autres espaces Rn. Mais du point du vue de la Géométrie différentielle il en va autrement. Les espaces numériques Rn sont naturellement munis d'une structure d'espace vectoriel, bien connue des élèves dès la 1re année de CPGE. Ca, c'est de l'Algèbre linéaire. Mais il existe d'autres structures, géométriques, en particulier celle de variété comme on l'a expliqué plus haut. Bien sûr tous les Rn sont munis canoniquement d'une structure de variété (il suffit de lire le début de cet article pour trouver ça évident, même sans connaître dans le détail la notion de variété). Phénomène incroyable : R⁴ est le SEUL a posséder d'autres structures de variété que la canonique. Ces structures ont été découvertes par S. Donaldson dans les années 80, on les appelle les structures exotiques. Il y en a une infinité. Pourquoi se fait ne se réalise qu'en dimension 4 ? Mystère…
De très belles vidéos expliquant la dimension 4 et les nombres complexes : dimensionsmaths

