Les polyèdres
La définition des polyèdres est assez compliquée. On peut la trouver dans des livres de Géométrie tel le célèbre Géométrie de Marcel BERGER (en deux tomes chez Nathan). La notion de polyèdre régulier est elle aussi délicate et nécessite des notions de théorie des groupes pour être énoncée clairement. Nous allons essayer de dégager ces notions.

Etymologie grecque pour comprendre :
- πολύς [polus] : nombreux.
- γωνία [gônia] : le coin, l'angle.
- χώρα [chôra] : la contrée, le pays, la région.
- ἕδϱα [hédra] : le siègle, la base. Noter qu'en français le H (représenté par l'accent en forme de lune sur le ε) a disparu. Il est conservé en anglais : polyhedron.
- τόπος [topos] : le lieu.
Les polygones
En dimension 2 les polyèdres sont des polygones.
Qu'est-ce qu'un polygone ? "une ligne brisée fermée" m'a un jour répondu un élève de 6e du collège Pierre de Geyter (Saint-Denis, 93) dans laquelle j'avais fait une intervension. En effet, un polygone est la donnée de deux choses :
- une liste finie ordonnée (S1, S2, ... , Sn) de points appelés sommets.
- une liste de segments, appelés arêtes ou côtés, reliant Sk à Sk+1 et Sn à S1. Il y a donc autant de d'arêtes que de sommets.
A ce titre, un polygone est un exemple de graphe (pour ceux qui connaissent le concept).
On connaît tous les célèbres polygones réguliers convexes :
-
n = 3 : triangle équilatéral
-
n = 4 : carré
-
n = 5 : pentagone
-
n = 6 : hexagone
-
n = 7 : heptagone
-
n = 8 : octogone
-
n = 9 : ennéagone
-
n = 10 : décagone
-
etc.
Pour n = 12 on parle de dodécagone et pour n = 20 on dit icosagone. Au delà, on dit «polygone à n côtés» ou «n-gone», même si l'on peut s'amuser à parler en grec. Par exemple, un 100-gone est un hectogone (ou hécatongone), un 1000-gone est un chiliogone, etc.
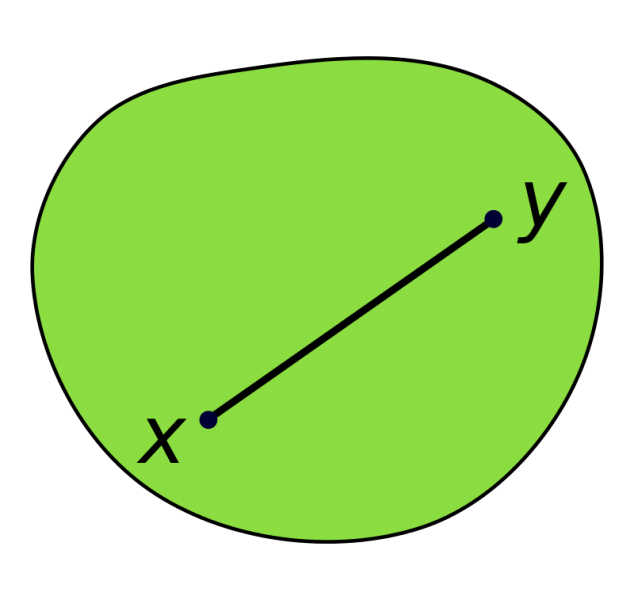
Que veut dire convexe ? Une partie P (par exemple un polygone) Si étant donnés deux points quelconques x et y dans P, le segment [xy] est totalement tracé dans P.
 |
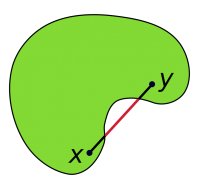 |
| partie convexe | partie non convexe |
Que veut dire régulier ? Un polygone P (convexe ou non) est dit régulier quand :
- tous ses sommets sont uniformes : deux sommets S1, S2 quelconques étant donnés, on peut trouver une rotation ou symétrie laissant invariant P qui envoie S1 sur S2
- toutes ses arêtes sont uniformes : deux arêtes A1, A2 quelconques étant données, on peut trouver une rotation ou une symétrie laissant invariant P qui envoie A1 sur A2
Attention : Il ne suffit pas que les arêtes soient de même longueur ! (Penser à un losange)
Un polygone est régulier exactement quand ses arêtes sont de mêmes longueur ET que tous ses angles sont identiques. C'est souvent cette définition qui est donnée, car elle est plus simple à appréhender.
Remarquons qu'il existe une infinité de polygones réguliers convexes. Ce fait est remarquable et ne s'étendra pas aux dimensions supérieures.
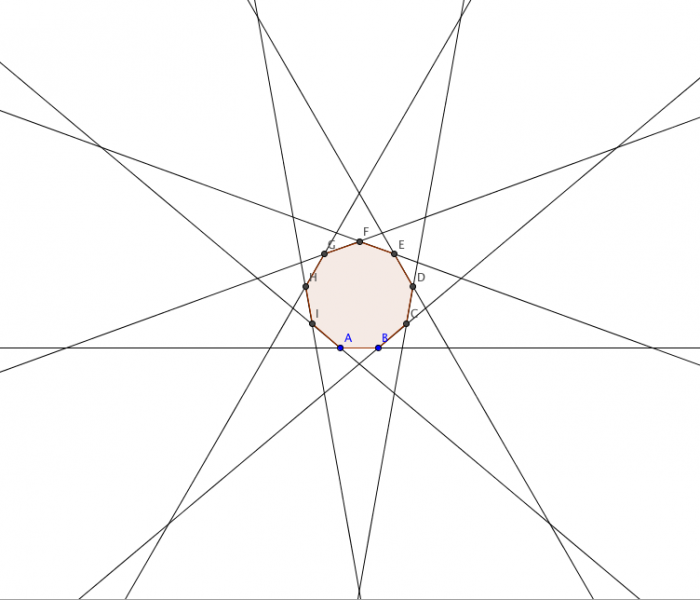
On peut aussi considérer des polygones réguliers étoilés (non convexes) en prolongeant les côtés jusqu'à ce qu'ils se retouchent : on appelle cela une stellation. Les plus connus sont l'étoile à 5 branches (le pentagramme) et l'étoile à 6 branches (l'hexagramme). Notons que l'hexagramme est particulier : c'est le composé de deux triangles équilatéraux, on ne peut pas partir d'un sommet, parcourir les arêtes et espérer passer par ses 6 sommets. On dit que c'est une stellation dégénérée.
L'heptagone possède 2 stellations représentées ci-dessous.
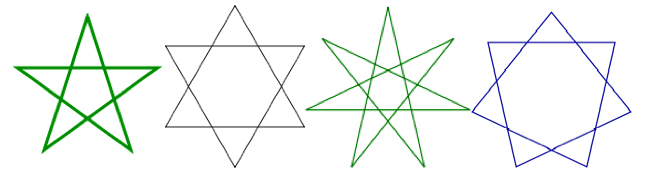
L'ennéagone en possède 3 (figure Géogébra ci-dessous), dont une dégénérée (l'intermédiaire sur la figure).
Pour codifer ces stellations, on utilise le symbole {n/m} où n est le nombre de côté du polygone de départ et m est le "pas" de la stellation, en convenant que m = 1 représente le premier pas de la stellation, c'est-à-dire le polygone de départ. Par exemple, les stellations représentées ci-dessus sont {5/2}, {6/2}, {7/3} et {7/2}, {9/2}, {9/3} et {9/4}.
On aura compris que {n/k} n'existe seulement quand k est un entier strictement inférieur à n/2, et que la stellation est non dégénérée quand n et k sont premiers entre eux. Par exemple, le 100-gone possède quant à lui 19 stellations non dégénérées : {100/k} avec k un entier entre 3 et 49 sauf les multiples de 2 et de 5.
Les polyèdres de Platon
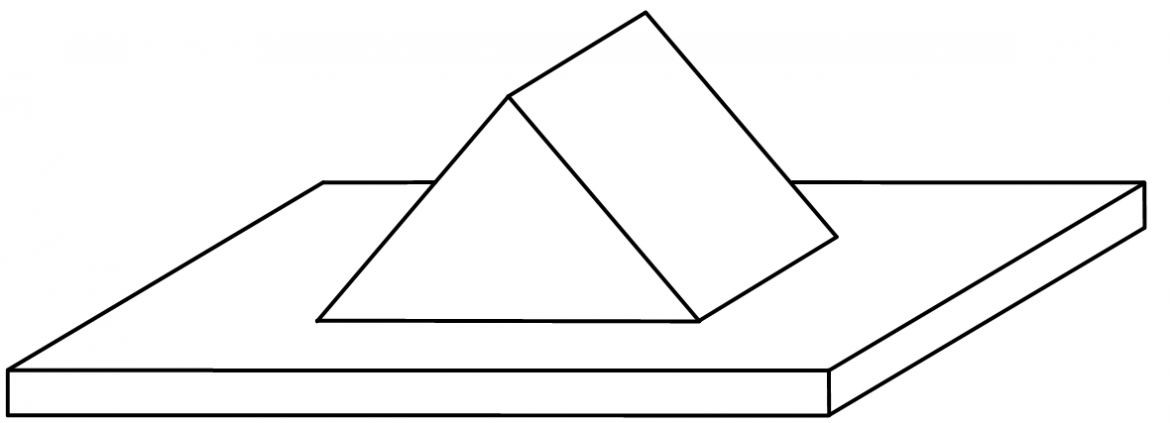
Le concept de polyèdre, bien que très intuitif, est difficile à défnir rigoureusement. Nous ne le ferons pas ici car cela nous emmènerait trop loin. Notons toutefois que toute figure de l'espace constituée de "faces planes" ne saurait être qualifiée de polyèdre comme le montre la figure ci-dessous :
La généralisation des polygones réguliers convexes à la dimension 3 est étonnante : il n'y a plus que 5 polygones réguliers convexes. Ils sont connus depuis longtemps, et le philosophe grec Platon leur a donné une signification mystique qu'il explique dans son dialogue Le Timée : feu, terre, air, éther (ou univers) et eau :
http://remacle.org/bloodwolf/philosophes/platon/cousin/timee.htm#170a
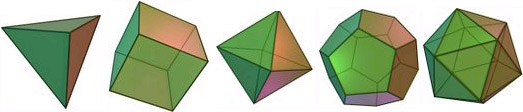
Ces 5 solides sont :
-
le tétraèdre, avec 4 faces qui sont des triangles, représente le feu
-
le cube, (ou hexaèdre) avec 6 faces qui sont des carrés, représente la terre
-
l'octaèdre, (ou le cocube) avec 8 faces qui sont des triangles, représente l'air
-
le dodécaèdre, avec 12 faces qui sont des pentagones, représente l'univers
-
l'icosaèdre, avec 20 faces qui sont des triangles, représente l'eau.
Un polyèdre (convexe ou non) P est dit régulier quand
- tous ses sommets sont uniformes : deux sommets S1, S2 quelconques étant donnés, on peut trouver une isométrie laissant invariant P qui envoie S1 sur S2
- toutes ses arêtes sont uniformes : deux arêtes A1, A2 quelconques étant données, on peut trouver une isométrie laissant invariant P qui envoie A1 sur A2
- toutes ses faces sont uniformes : deux faces F1, F2 quelconques étant donnése, on peut trouver une isométrie laissant invariant P qui envoie F1 sur F2
Intuitivement, dans un polyèdre régulier toutes les faces sont “agencées” de la même façon. En particulier, de chaque sommet partent un même nombre de arêtes (3 pour le tétraèdre, le cube et le dodécaèdre, par exemple).
Les polyèdres de Kepler-Poinsot
On peut alors s'interroger sur l'existence de stellations des polyèdres, en prolongeant leurs faces jusqu'à ce qu'elles se rencontrent. On constate facilement que
- le tétraèdre n'admet pas de stellation, à l'instar de son homologue polygonal : le triangle équilatéral.
- le cube n'admet pas de stellation, à l'instar de son homologue polygonal : le carré. En effet, les faces d'un cube sont parallèles !
- l'octaèdre possède une stellation : l'octangle étoilé (stella octangula), ou étoile de Kepler, représentée ci-dessous. Notons que l'octangle n'est pas un polyèdre régulier.
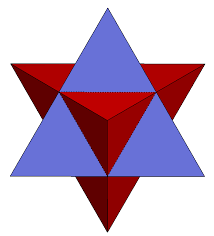 |
 |
 |
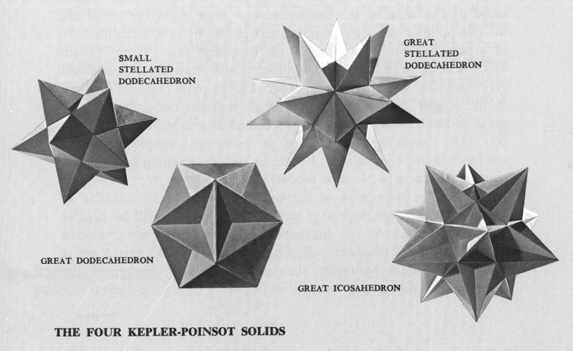
- le dodécaèdre possède 3 stellations, qui sont toutes des polyèdres réguliers, mais non convexes. Il s'agit du Grand dodécaèdre, du Petit dodécaèdre étoilé et du Grand dodécaèdre étoilé. L'adjectif "étoilé" est là pour signaler que les faces sont des pentagones étoilés {5/2}. Ainsi, le Grand dodécaèdre a des faces qui sont des pentagones "vrais" (non étoilés).
 |
 |
 |
- l'icosèdre possède... 58 stellations ! Seule l'une d'entre elles est régulière : le Grand Icosaèdre. A sa gauche, ci-dessous, on a représenté la dernière stellation de l'icosaèdre : l'icosaèdre complet.
 |
 |
En 1619 Kepler a découvert deux stellations régulières : le Grand et le Petit dodécaèdres étoilés.
En 1809, Louis Poinsot en trouve deux autres, d'apparence peut-être un peu plus compliquée par la présence de "faces évidées".
En 1812, Augustin Louis Cauchy (célèbre dans les cours de Maths en prépa !) démontra que la liste était complète !
Depuis, ces 4 polyèdres réguliers non convexes s'appellent les poylèdres de Kepler-Poinsot.
Le petit dodécaèdre étoilé a 12 faces qui sont des pentagones étoilés
Le grand dodécaèdre étoilé a 12 faces qui sont aussi des pentagones étoilés
Le grand dodécaèdre a 12 faces qui sont des pentagones (convexes)
Le grand icosaèdre a 20 faces qui sont des triangles équilatéraux.
Les deltaèdres
Comme leur nom l'indique, les deltaèdres sont des polyèdres sont des triangles équilatéraux. On peut montrer qu'il y a :
-
- 8 deltaèdres convexes,
-
- une infinité de deltaèdres non convexes.

Remarquons que le nombre de faces est toujours pair, va de 2 en 2 de 4 à 20 mais ne prend pas la valeur 18 ! Pourquoi ? …
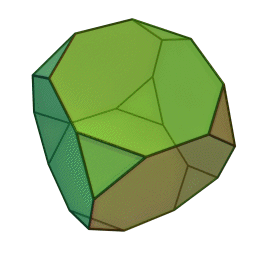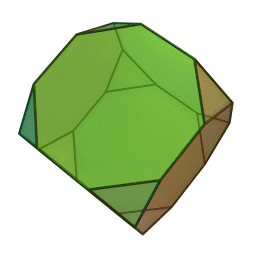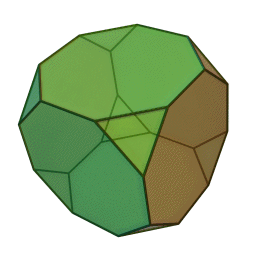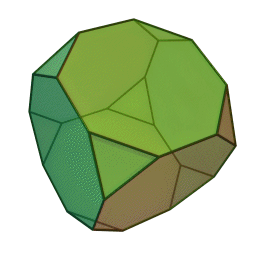
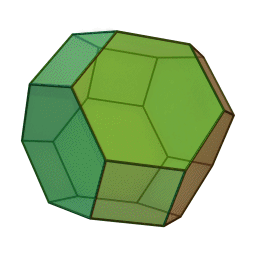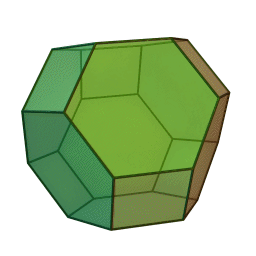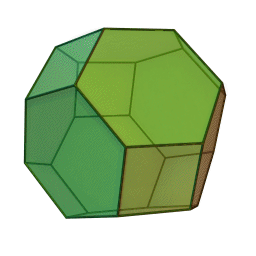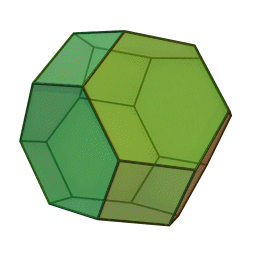
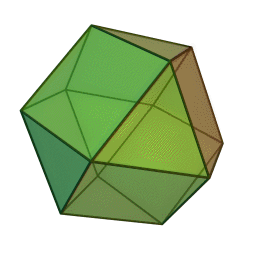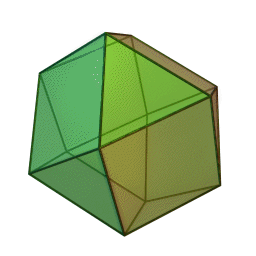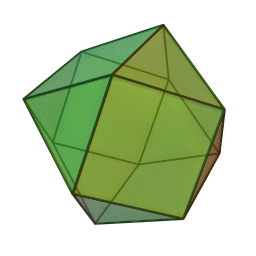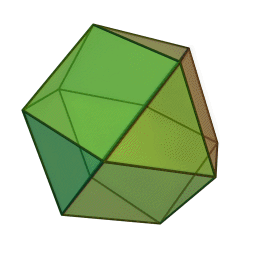
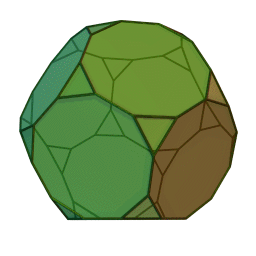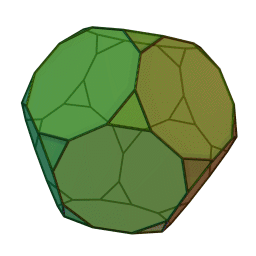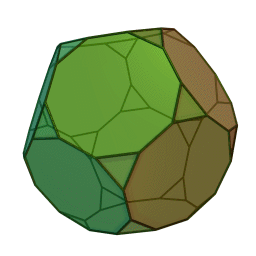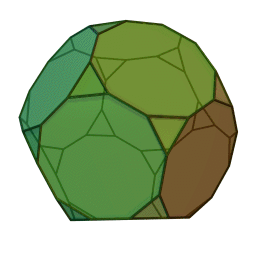
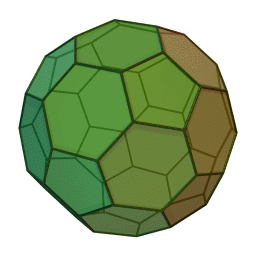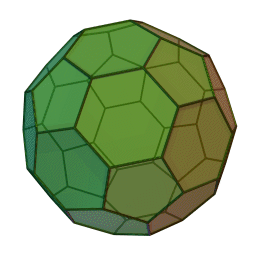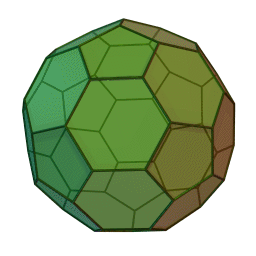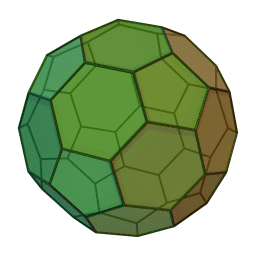
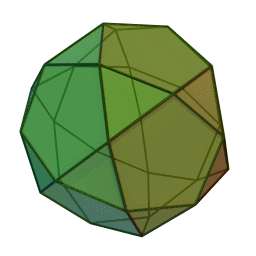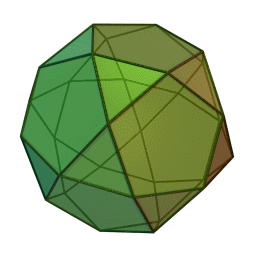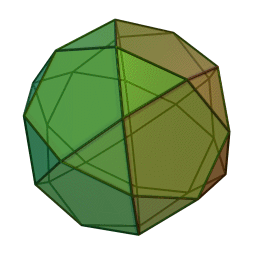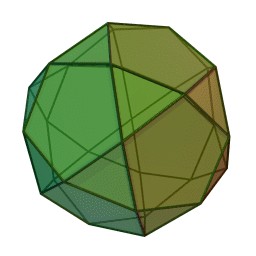
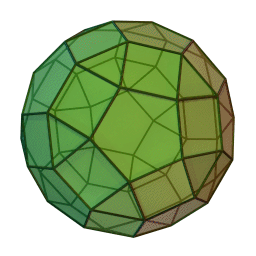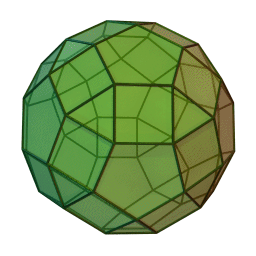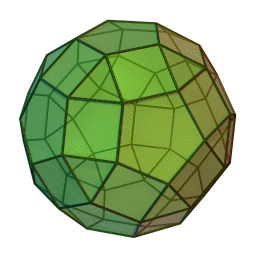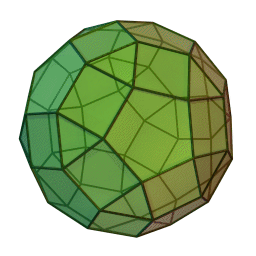
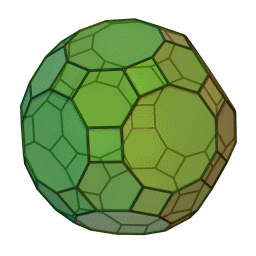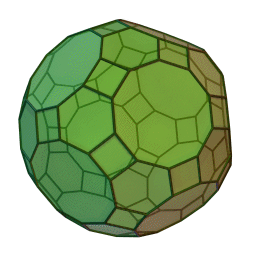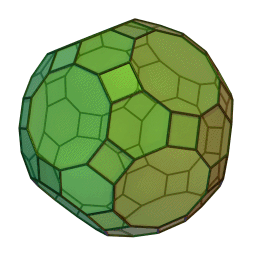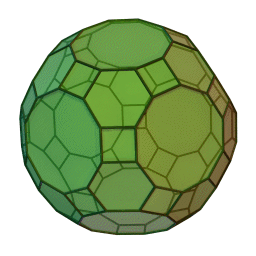
Les polyèdres archimédiens
Ce sont des polyèdres convexes dont les faces sont assemblées de la même façon, tout comme les polyèdres de Platon, mais qui peuvent avoir des faces différentes, tout en restant des polygones réguliers. On peut démontrer qu'il y en a 13 (+ 2 versions "miroirs" de deux d'entre eux) dont le célèbre "ballon de foot" composé d'hexagones (blancs) et de pentagones (noirs).
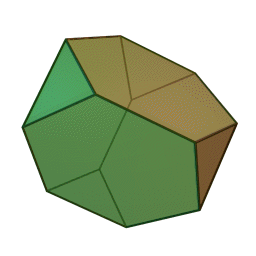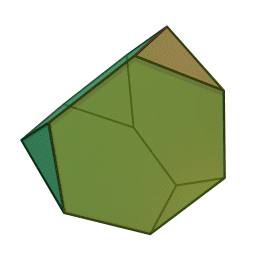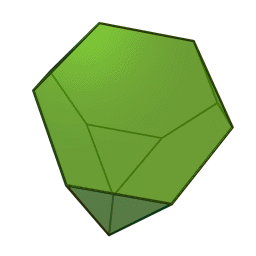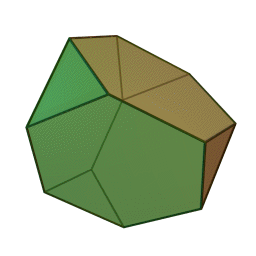 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
D'autres polyèdres
-
Les 92 solides de Johnson. Le mathématicien Norman Johnson s'est intéressé aux polyèdres strictement convexe dont chaque face est un polygone régulier (pas forcément le même) et qui ne sont pas un polyèdre de Platon ou d'Archimède, un prisme ou un antiprisme. Il en dressa la liste en 1966 et c'est un autre mathématicien, Victor Zalgaller, qui démontra en 1969 que cette liste était complète. Un exemple simple est par exemple la pyramide à base carrée dont les faces sont des triangles équilatéraux. Il semble que tout est possible, mais en fait on peut démontrer que les faces ont nécessairement 3, 4, 5, 6, 8 ou 10 côtés. Pour voir la liste complète des solides de Johnson cliquez ici.

-
Les 13 polyèdres semi-réguliers de Catalan. Il s'agit des duals des polyèdres archimédiens. La dualité est assez compliquée à définir dans le cas général (cliquez ici) mais pour les polyèdres réguliers, les duals s'obtiennent en reliant les centres des faces : ainsi le dual du cube est un octaèdre (c'est pour cela qu'on l'appelle souvent le co-cube). Les polyèdres de Catalan ne sont pas réguliers car il arrive que leurs faces ne soient pas des polygones réguliers. Pour voir leur liste cliquez ici.
Voici un site où l'on peut trouver beaucoup de patrons pour construire, avec du papier, des ciseaux, de la colle et … beaucoup de patience, des polyèdres (en illustration : un exemple) : http://www.korthalsaltes.com/
On peut aussi créer un Grand Dodécaèdre Etoilé en origami modulaire c'est-à-dire sans colle, juste en pliant du papier : il suffit de plier 30 carrés comme l'indique le fichier → ici ← et de les assembler pour former le polyèdre.
Un ballon de foot géant (vidéo) : M. Gaudel, professeur au lycée Louise Michel de Bobigny, construit avec ses élèves de RENCONTRES CNRS SCIENCES JEUNES ET CITOYENS à Poitier un «ballon de foot» géant. C'est un polyèdre archimédien construit à l'aide de baguettes et de ficelle. Impressionnant !
Cliquez ici Cliquez ici pour voir la vidéo.

Polyèdres en toute dimension
La notion de polyèdre se généralise aux dimensions supérieures : on parle alors de polytopes. En dimension 4 on peut aussi parler de polychores (en grec, topos : le lieu et chôra : la région). En dimension n, un polytope possède des sommets (ou 0-cellules), des arêtes (ou 1-cellules), des faces (ou 2-cellules), etc. jusqu'aux (n-1)-cellules. Le nombre de (n-1)-cellules donne en général le nom du polytopes, exactement comme en dimension 2 et 3.
On s'est alors intéressé à la classification des polyèdres réguliers, convexes et étoilés. Le résultat est surprenant !
- ?le n-simplexe généralise le tétraèdre : il possède n+1 sommets et autant de (n-1)-cellules.
- l'hypercube (ou n-cube) : il possède 2n sommets et 2n (n-1)-cellules.
- l'hyperoctaèdre (ou n-cocube) : il possède 2n sommets?? et 2n (n-1)-cellules. Notons la dualité entre cube et cocube.
- ?le 4-simplexe s'appelle ici pentachore : il possède 5 sommets mais surtout 5 cellules (faces 3D), d'où son nom.
- le 4-cube s'appelle ici tesseract. C'est une star : il a joué un rôle dans le film The Avengers (2012). On l'appelle aussi octachore car il possède 8 cellules.
- le 4-cocube s'appelle ici hexadécachore parce qu'il possède 16 cellules.
Puis, parmi les trois polychores exceptionnels on trouve : - l'icositétrachore qui a 24 cellules comme son nom l'indique.
- l'hécatonicosachore qui a 120 cellules.
- l'hexacosichore qui a... 600 céellules !
On peut représenter les polychores par projections dans l'espace de dimenion 3.
 |
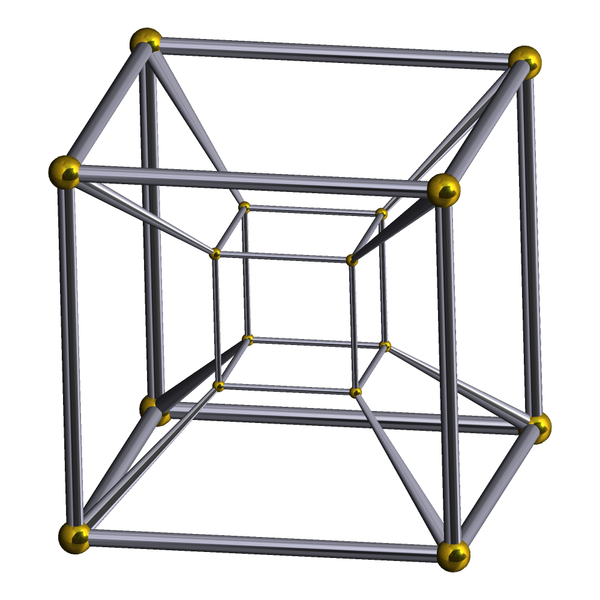 |
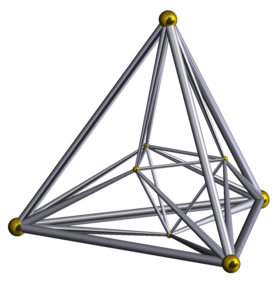 |
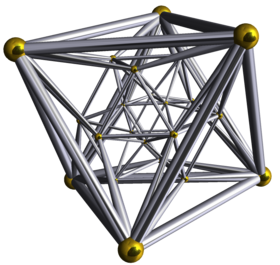 |
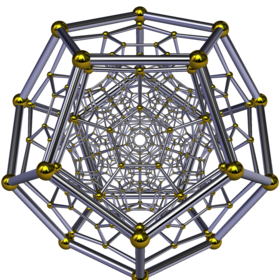 |
 |
Il est bien sûr difficile de s'imaginer le rendu réel en dimension 4. A titre de comparaison, si on projette un tétraèdre ou un cube dans le plan, on obtient les figures "peu parlantes" suivantes :
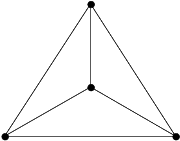 |
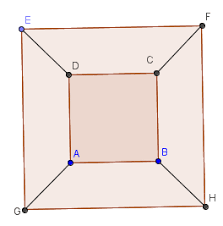 |
| projection plane d'un tétraèdre | projection plane d'un cube |
Parmi les stellations des six polychores convexes, on dénombre 10 polychores étoilés provenant uniquement des stellations de l'hécatonicosachore (120 cellules) et de l'hexacosichore (600 cellules).
?
On doit ces résultats au mathématicien suisse Ludwig Schläfli (1814-1895).